Trigonometry Function Formulas – Math Shortcut Tricks

Trigonometry Function Formulas

So, here are few Trigonometry Function Formulas. Let’s learn some basics of these formulas.

Trigonometry Function Formulas of a Right Triangle :

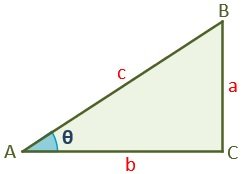
sin α = a / c = opposite / hypotenuse
cos α = b / c = adjacent / hypotenuse
tan α = a / b = opposite / adjacent

cot α = b / a = adjacent / opposite

sec α = c / b Cosec α = c / a

Basic Formula :

sin² α + cos² α = 1

tan α . cot tan α = 1

tan α = sin α / cos α = 1 / cot tan α

cot tan α = cos α / sin α = 1 / tan α

1 + tan² α = 1 / cos² α = sec² α

1 + cot tan² α = 1 / sin² α = cos sec² α

Trigonometric Table

α	00	300	450	600	900	1200	1800	2700	3600
sin α	0	1/2	√2/2	√3/2	1	√3/2	0	-1	0
cos α	1	√3/2	√2/2	1/2	0	-1/2	-1	0	1
tan α	0	1/√3	1	√3	∞	-√3	0	∞	0
cot α	∞	√3	1	1/√3	0	-1/√3	∞	0	∞
sec α	1	2/√3	√2	2	∞	-2	-1	∞	1
cosec α	∞	2	√2	2/√3	1	2/√3	∞	-1	∞

Co-Ratios

	sin	cos	tan	cot
-α	-sin α	+cos α	-tan α	-cot α
900 – α	+cos α	+sin α	+cot α	+tan α
900 + α	+cos α	-sin α	-cot α	-tan α
1800 – α	+sin α	-cos α	-tan α	-cot α
1800 + α	-sin α	-cos α	+tan α	+cot α
2700 – α	-cos α	-sin α	+cot α	+tan α
2700 + α	-cos α	+sin α	-cot α	-tan α
3600k – α	-sin α	+cos α	-tan α	-cot α
3600k – α	+sin α	+cos α	+tan α	+cot α

Trigonometry Addition Formula:

• sin(A + B) = sinA cosB + cosA sinB
• sin(A – B) = sinA cosB – cosA sinB

• cos(A + B) = cosA cosB – sinA sinB
• cos(A – B) = cosA cosB + sinA sinB

• tan (A + B) = tanA + tanB / 1 – tanA tanB
• tan(A – B) = tanA – tanB / 1 + tanA tanB

• cot (A+ B) = cotA cotB – 1 / cotA + cotB

Product of Trigonometric Functions:

• sin α cos β = 1/2 [ sin (α + β) + sin(α – β)]
• cos α sin β = 1/2 [ sin (α + β) – sin(α – β)]
• cos α cos β = 1/2 [ cos (α + β) + cos(α – β)]
• sin α sin β = 1/2 [ cos (α – β) – cos(α + β)]

• tan α tan β = tan α + tan β / cot tan α + cot tanβ = – tanα – tan β / cot tan α – cot tan β

Trigonometric Formula with t = tan(x/2)

sinx = 2t / 1 + t²

cos x = 1 – t² / 1 + t²

tan x = 2t / 1 – t²

cot x = 1 – t² / 2t

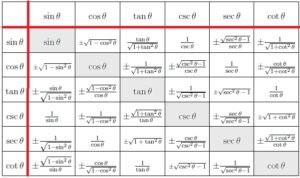
Trigonometric Relation Between Functions:

Angle of a Plane Triangle :

• A, B, C are 3 angles of a triangle
• sin A + sin B + sin c = 4 cos(A / 2) cos(B/2) cos(C/2)
• cosA + cos B + cos C = 4 sin(A/2) sin(B/2) sin(C/2) + 1
• sinA + sinB – sinC = 4sin (A/2) sin (B/2) cos (C/2)

And, please visit this page to get more updates on Math Shortcut Tricks and Trigonometry Function Formulas. You can also like our facebook page to get updates.

So, if you have any question regarding Trigonometry Function Formulas then please do comment on below section.